Expected frequency of species

Given a community size, biodiversity parameter \(\theta\), and an immigration rate \(m\), returns the expected frequency of species with \(n\) individuals, for \(0<n\leq J\).

Usage

volkov(J, params, bins = FALSE, give = FALSE)

Arguments

J: Size of community
params: A two-element vector with first element interpreted as theta, the Fundamental biodiversity parameter and the second, m, interpreted as the probability of immigration. This argument will accept the output of optimal.params()
bins: Boolean, with default FALSE meaning to return the expected number of species with \(1,2,\ldots,J\) individuals, and FALSE meaning to return the binned total, using a Preston-like binning system as used in preston()
give: Boolean, with TRUE meaning to return all the output of integrate(), and default FALSE meaning to return just the value of the integral

Value

Returns an object of class “phi”.

References

I. Volkov and others 2003. “Neutral theory and relative species abundance in ecology”. Nature, volume 424, number 28.

Author

Robin K. S. Hankin

Note

The method used is slightly inefficient: the terms to the left of the integral sign [in Volkov's equation 7] are integrated and this is, strictly, unnecessary as it is not a function of \(y\). However, taking advantage of this fact results in messy code.

Examples

if (FALSE) { # \dontrun{
  volkov(J=21457,c(theta=47.226, m=0.1)) # Example in figure 1
} # } 

volkov(J=20,params=c(theta=1,m=0.4))
#>  [1] 0.59067733 0.36193725 0.25810432 0.19659328 0.15567107 0.12660270
#>  [7] 0.10504586 0.08854998 0.07561319 0.06526131 0.05683587 0.04987788
#> [13] 0.04405974 0.03914391 0.03495774 0.03138073 0.02834761 0.02589611
#> [19] 0.02447062 0.03341949

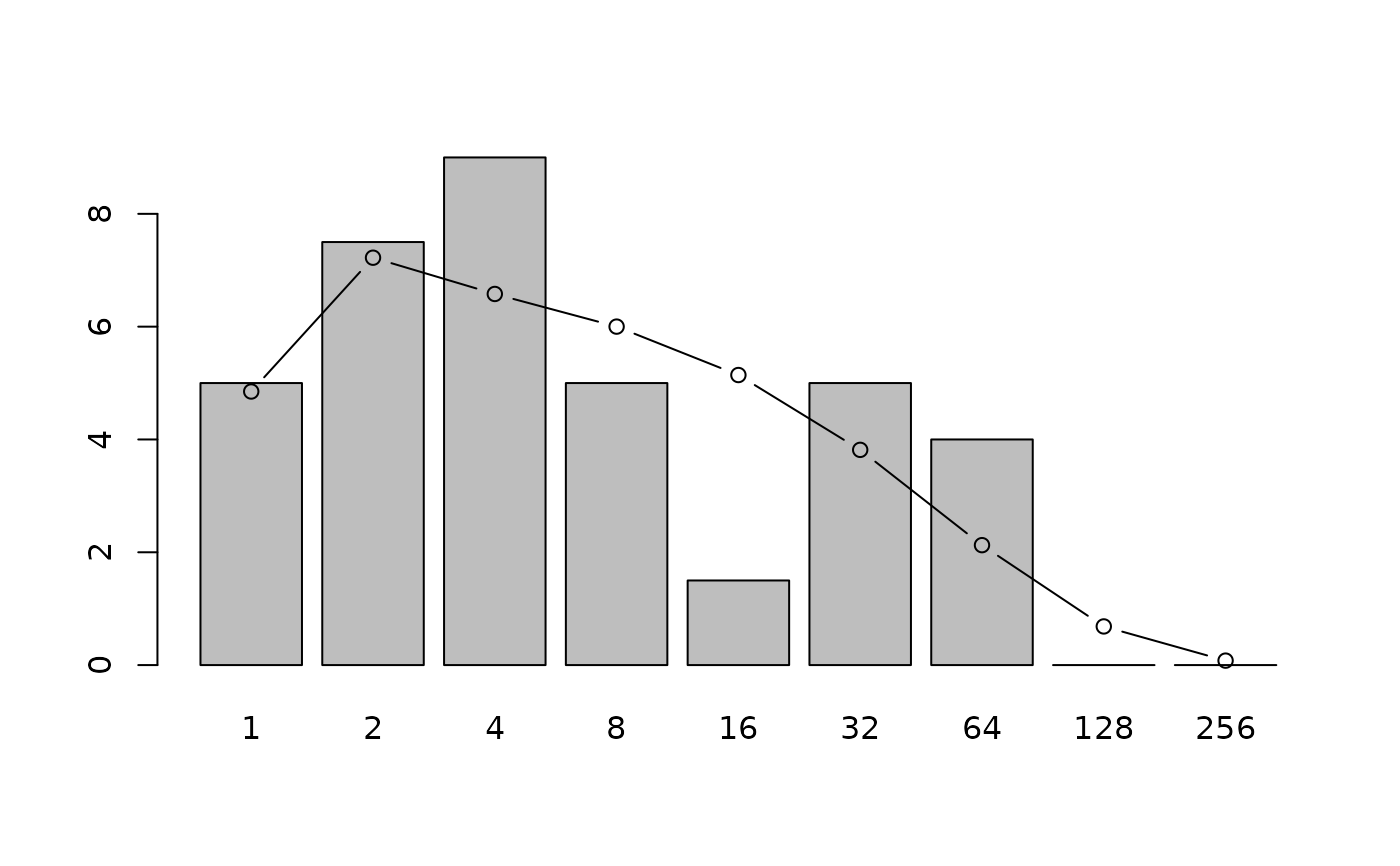
 data(butterflies)
 r <- plot(preston(butterflies,n=9,orig=TRUE))

 if (FALSE)   jj <- optimal.params(butterflies)   # \dontrun{}  # needs PARI/GP

 jj <- c(9.99980936124759, 0.991791987473506)

 points(r,volkov(no.of.ind(butterflies), jj, bins=TRUE),type="b")