Permutation matrices — perm_matrix • permutations

Given a permutation, coerce to word form and return the corresponding permutation matrix

Usage

perm_matrix(p,s=size(p))
is.perm_matrix(M)
pm_to_perm(M)

Arguments

p: Permutation, coerced to word form, of length 1
s: Size of permutation matrix or permutation
M: Permutation matrix

Details

Given a permutation p of size \(s\), function perm_matrix() returns a square matrix with \(s\) rows and \(s\) columns. Entries are either 0 or 1; each row and each column has exactly one entry of 1 and the rest zero.

Row and column names of the permutation matrix are integers; this makes the printed version more compact.

Function pm_to_perm() takes a permutation matrix and returns the equivalent permutation in word form.

Note

Given a word p with size s, the idiom for perm_matrix() boils down to


    M <- diag(s)
    M[p,]

This is used explicitly in the representations vignette. There is another way:


    M <- diag(s)
    M[cbind(seq_len(s),p)] <- 1
    M

which might be useful sometime.

See also the representation and order_of_ops vignettes, which discuss permutation matrices.

Author

Robin K. S. Hankin

Examples


perm_matrix(rperm(1,9))
#>   1 2 3 4 5 6 7 8 9
#> 1 0 0 0 1 0 0 0 0 0
#> 2 1 0 0 0 0 0 0 0 0
#> 3 0 1 0 0 0 0 0 0 0
#> 4 0 0 0 0 0 0 0 0 1
#> 5 0 0 0 0 0 0 1 0 0
#> 6 0 0 0 0 0 1 0 0 0
#> 7 0 0 0 0 1 0 0 0 0
#> 8 0 0 0 0 0 0 0 1 0
#> 9 0 0 1 0 0 0 0 0 0


p1 <- rperm(1,40)
M1 <- perm_matrix(p1)
p2 <- rperm(1,40)
M2 <- perm_matrix(p2)

stopifnot(is.perm_matrix(M1))

stopifnot(all(solve(M1) == perm_matrix(inverse(p1))))
stopifnot(all(M1 %*% M2 == perm_matrix(p1*p2)))


stopifnot(p1 == pm_to_perm(perm_matrix(p1)))

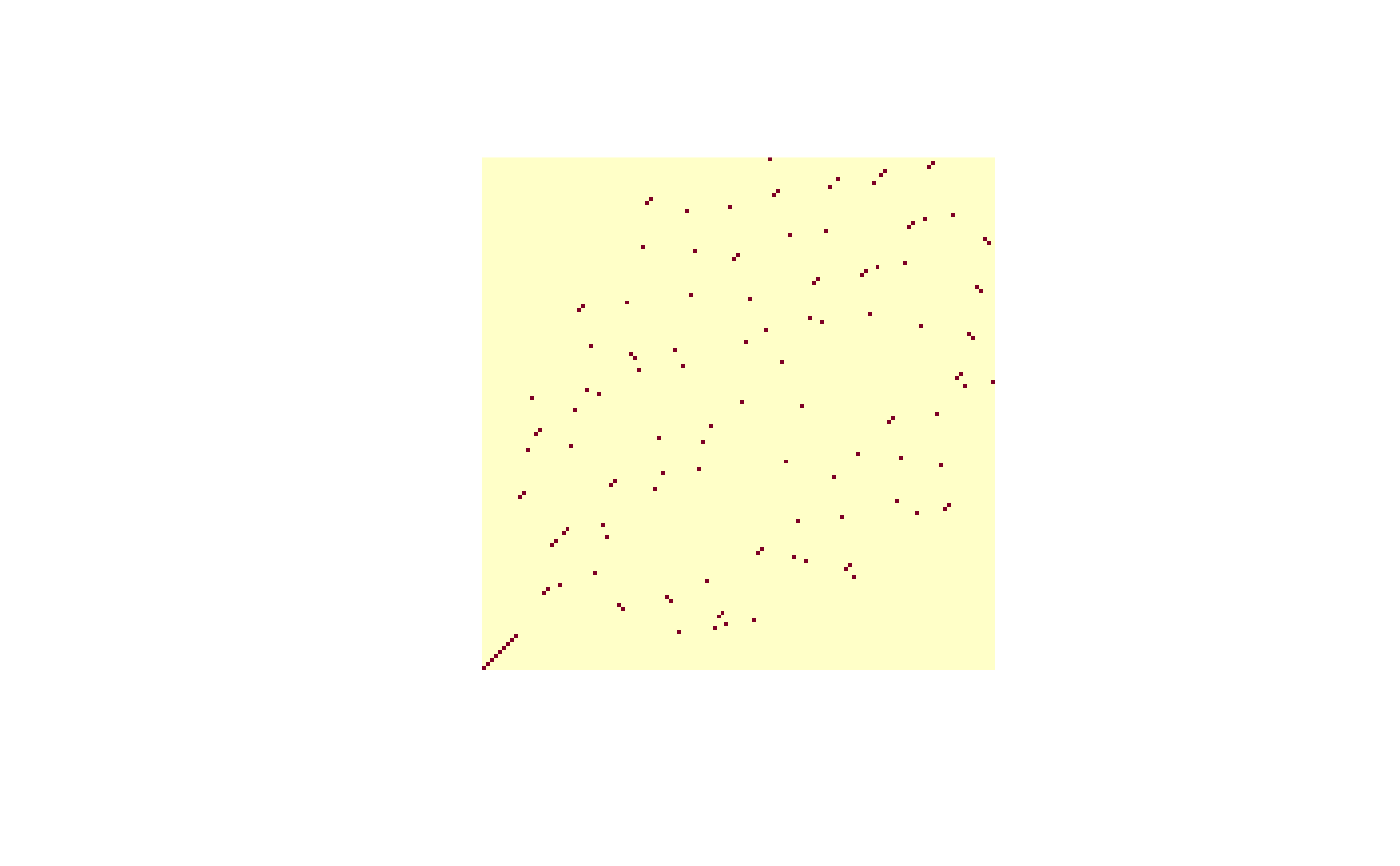
data("megaminx")
image(perm_matrix(permprod(megaminx)),asp=1,axes=FALSE)