Unimodular matrices

Systematically generates unimodular matrices; numerical verification of a function's unimodularness

unimodular(n)
unimodularity(n,o, FUN, ...)

Arguments

n

Maximum size of entries of matrices

o

Two element vector

FUN

Function whose unimodularity is to be checked

...

Further arguments passed to FUN

Details

Here, a ‘unimodular’ matrix is of size \(2\times 2\), with integer entries and a determinant of unity.

Value

Function unimodular() returns an array a of dimension c(2,2,u) (where u is a complicated function of n). Thus 3-slices of a (that is, a[,,i]) are unimodular.

Function unimodularity() returns the result of applying FUN() to the unimodular transformations of o. The function returns a vector of length dim(unimodular(n))[3]; if FUN() is unimodular and roundoff is neglected, all elements of the vector should be identical.

Author

Robin K. S. Hankin

Note

In function as.primitive(), a ‘unimodular’ may have determinant minus one.

See also

as.primitive

Examples

unimodular(3)
#> , , 1
#> 
#>      [,1] [,2]
#> [1,]    1    0
#> [2,]    0    1
#> 
#> , , 2
#> 
#>      [,1] [,2]
#> [1,]    1    1
#> [2,]    0    1
#> 
#> , , 3
#> 
#>      [,1] [,2]
#> [1,]    1    2
#> [2,]    0    1
#> 
#> , , 4
#> 
#>      [,1] [,2]
#> [1,]    2    1
#> [2,]    1    1
#> 
#> , , 5
#> 
#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    0    1
#> 
#> , , 6
#> 
#>      [,1] [,2]
#> [1,]    3    2
#> [2,]    1    1
#> 
#> , , 7
#> 
#>      [,1] [,2]
#> [1,]    2    3
#> [2,]    1    2
#> 
#> , , 8
#> 
#>      [,1] [,2]
#> [1,]    3    1
#> [2,]    2    1
#> 

o <- c(1,1i)
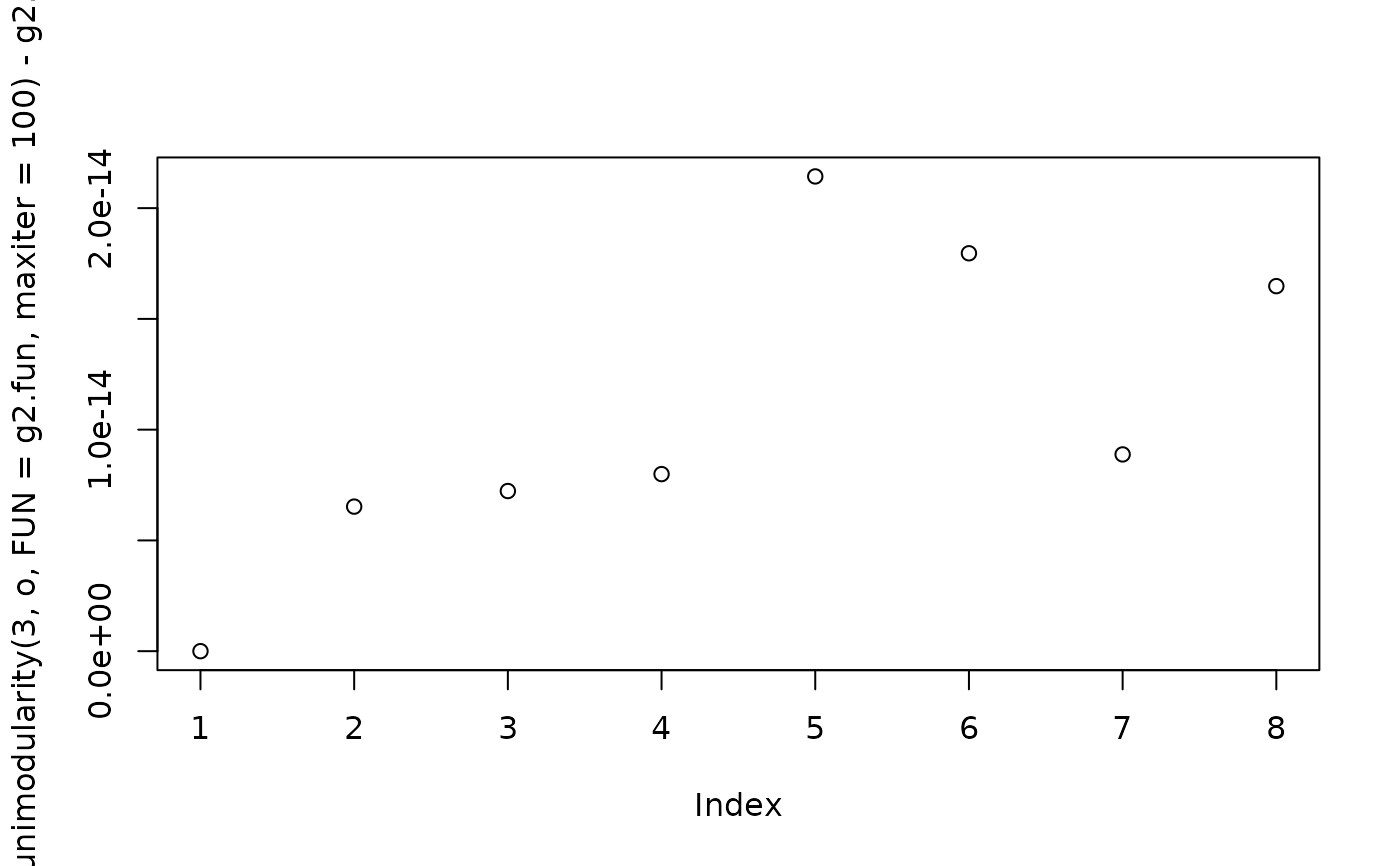
plot(abs(unimodularity(3,o,FUN=g2.fun,maxiter=100)-g2.fun(o)))