Skip to contents

Random neutral ecosystem

rand.neutral.Rd

Given the size of the metacommunity \(J\), and the fundamental biodiversity number \(\theta\), generate an object of class count using a stochastic mechanism consistent with the neutral theory.

Usage

rand.neutral(J, theta=NULL, prob.of.mutate=NULL, string = NULL, pad = FALSE)

Arguments

J

Size of metacommunity

theta

Fundamental biodiversity number \(\theta\). User must supply exactly one of theta and prob.of.mutate.

prob.of.mutate

Probability of mutation \(\nu\): \(\theta=2J\nu\).

string

String to add to species names. By default (ie string being NULL), species are named “1”, “2”,\(\ldots\). Argument string supplies a prefix for these species names; a good one to use is “spp.”. This argument is useful because printing a count object can be confusing if the species names are all integers.

pad

Boolean, with default FALSE meaning to return a count object having only extant species, and TRUE meaning to pad the count with extinct species to J species. Use this when a vector of length J is required consistently (see examples section).

Details

Uses the simulation method on page 289 of Hubbell (2001).

Note

If pad is TRUE, and you set string to “extinct”, things will break.

References

S. P. Hubbell 2001. “The Unified Neutral Theory of Biodiversity”. Princeton University Press.

Author

Robin K. S. Hankin

See also

untb

Examples

rand.neutral(1000, 9)
#>   2   7   4   1   8   6  10  11  13   5   3  18  14  17  15  12  23   9  16  20 
#> 269 130 122  87  82  66  43  39  35  21  20  16  14  14  12   9   3   2   2   2 
#>  29  30  19  21  22  24  25  26  27  28 
#>   2   2   1   1   1   1   1   1   1   1 
rand.neutral(1000, 9, string="spp.")
#>  spp.5 spp.10  spp.9  spp.8  spp.1 spp.12 spp.16 spp.11  spp.7 spp.13 spp.19 
#>    135    116    105     83     78     72     45     41     41     39     30 
#> spp.17  spp.4 spp.18  spp.6  spp.3 spp.15 spp.23 spp.20 spp.21 spp.26 spp.28 
#>     29     29     25     17     15     14     14     12     10      6      6 
#> spp.24 spp.25 spp.32 spp.14 spp.31  spp.2 spp.22 spp.29 spp.33 spp.38 spp.39 
#>      5      4      4      3      3      2      2      2      2      2      2 
#> spp.27 spp.30 spp.34 spp.35 spp.36 spp.37 spp.40 
#>      1      1      1      1      1      1      1 

data(butterflies)
rand.neutral(no.of.ind(butterflies), optimal.theta(butterflies),string="spp.")
#>  spp.5  spp.4  spp.2 spp.12 spp.11  spp.8 spp.17  spp.6 spp.25  spp.3 spp.15 
#>     75     37     36     34     20     17     16     15     14     12      9 
#> spp.14 spp.19  spp.1 spp.13 spp.22 spp.26 spp.23 spp.24 spp.30 spp.10 spp.16 
#>      8      8      7      7      6      6      4      4      4      3      3 
#> spp.21 spp.29 spp.31 spp.37 spp.20 spp.27 spp.32 spp.34 spp.36  spp.9 spp.18 
#>      3      3      3      3      2      2      2      2      2      2      1 
#> spp.28 spp.33 spp.35 spp.38 spp.39  spp.7 
#>      1      1      1      1      1      1 


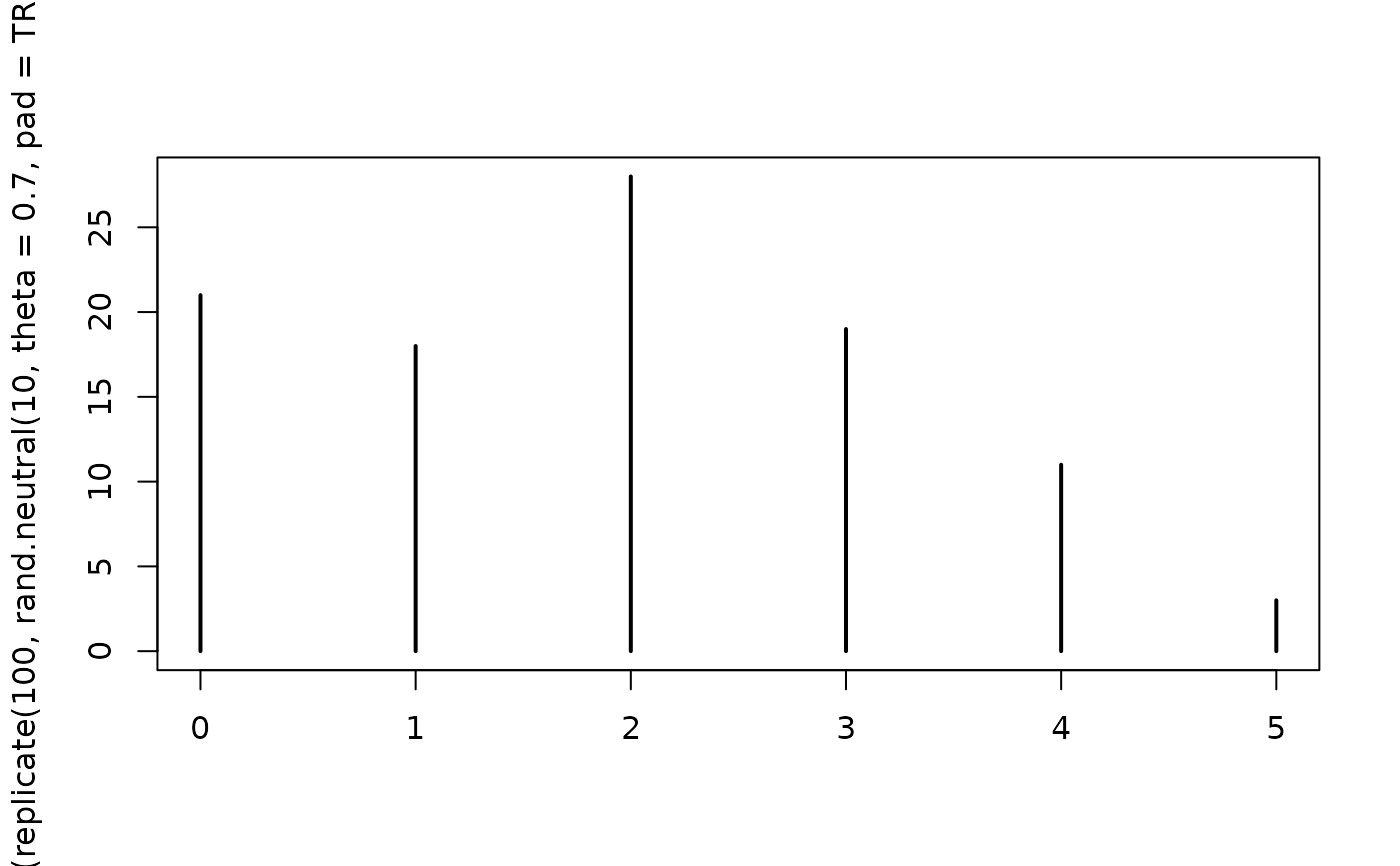
# what is the distribution of abundance of the second ranked species if
# J=10, theta=0.7?
plot(table(replicate(100,rand.neutral(10,theta=0.7,pad=TRUE)[2])))