Generating function for a chess knight and king
knight.RdGenerating function for a chess knight and king on an arbitrarily-dimensioned chessboard
Note
The pieces are forced to move; if they have the option of not moving, add 1 to the returned spray. The vignette contains a short discussion.
Examples
knight() # default 2D chess board
#> val
#> -1 2 = 1
#> 2 -1 = 1
#> -2 1 = 1
#> -1 -2 = 1
#> -2 -1 = 1
#> 1 2 = 1
#> 1 -2 = 1
#> 2 1 = 1
king() # ditto
#> val
#> 1 1 = 1
#> 0 1 = 1
#> -1 1 = 1
#> 1 0 = 1
#> -1 0 = 1
#> 1 -1 = 1
#> 0 -1 = 1
#> -1 -1 = 1
knight()^2 # generating function for two knight's moves
#> val
#> 3 3 = 2
#> -1 -3 = 2
#> -1 1 = 2
#> -2 -4 = 1
#> 3 -3 = 2
#> -1 -1 = 2
#> -3 -3 = 2
#> 2 -4 = 1
#> 1 -1 = 2
#> -1 3 = 2
#> 1 -3 = 2
#> -3 3 = 2
#> 4 -2 = 1
#> 3 1 = 2
#> -2 0 = 2
#> 2 4 = 1
#> 3 -1 = 2
#> 0 -4 = 2
#> 0 0 = 8
#> 4 0 = 2
#> -3 1 = 2
#> 1 3 = 2
#> -4 -2 = 1
#> 0 2 = 2
#> 4 2 = 1
#> -3 -1 = 2
#> 1 1 = 2
#> 0 4 = 2
#> -2 4 = 1
#> 2 0 = 2
#> -4 0 = 2
#> 0 -2 = 2
#> -4 2 = 1
## How many ways can a knight return to its starting square in 6 moves?
constant(knight()^6)
#> val
#> 0 0 = 5840
## How many in 6 or fewer?
constant((1+knight())^6)
#> val
#> 0 0 = 8481
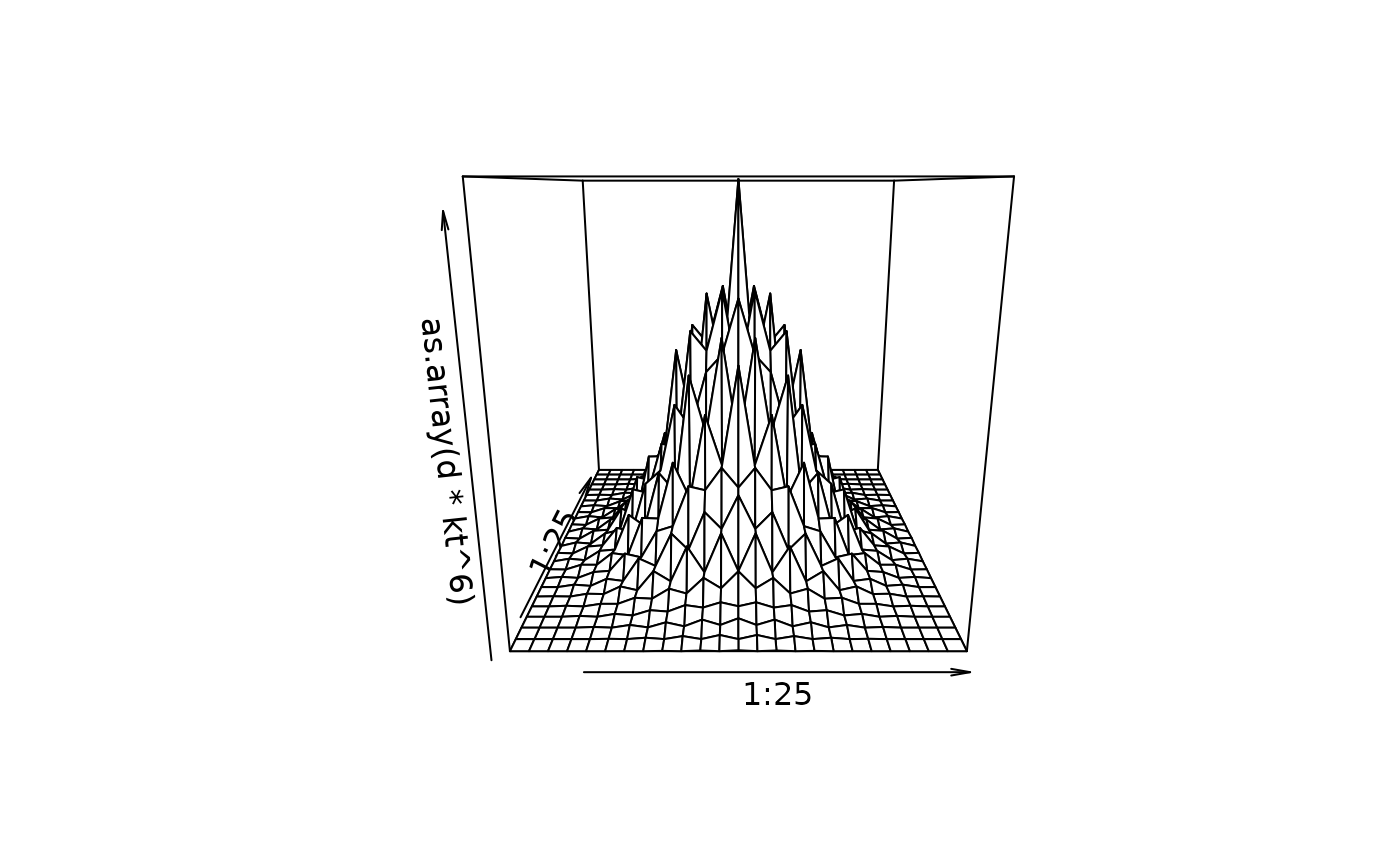
## Where does a randomly-moving knight end up?
d <- xyz(2)
kt <- (1+knight())*d^2/9
persp(1:25,1:25,as.array(d*kt^6))
## what is the probability that a 4D king is a knight's move from
## (0,0,0,0) after 6 moves?
sum(coeffs(((king(4)/80)^4)[knight(4)]))
#> [1] 0.06367969